Implement a Binary Tree in Golang

The biggest challenge in Computer Science is transforming a data structure that has a complexity of O(n) to O(log n), this is not an easy journey. In this post we will discover how the binary tree does this (at least tries to) and implement this data structure using Golang.

Introduction to Binary Trees

A binary tree is a hierarchical data structure where each node has at most two children: a left child and a right child. This structure allows binary trees to maintain a sorted order, making search operations efficient.

One thing important isn't confuse the Binary Tre

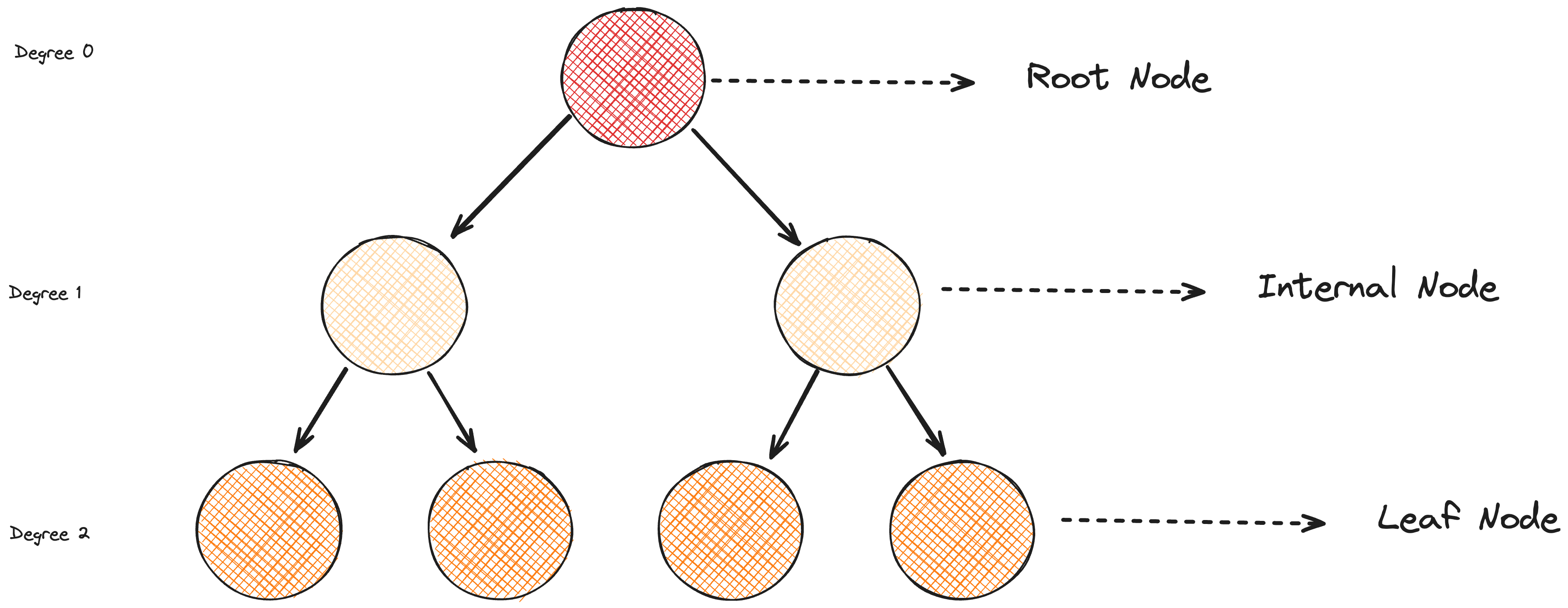
Binary Tree Concepts and Terminology

Before diving into the implementation, let's go over some key concepts and terminology:

• Root: The topmost node of the tree.
• Node: The basic unit of a binary tree, containing a value and pointers to its children.
• Leaf Node: A node with no children.
• Height: The number of edges on the longest path from the node to a leaf.

Setting Up the Golang Environment

Before we start, ensure you have Golang installed. You can download it from the official website here.

To set up your project, create a new directory and initialize a Go module:

mkdir binarytree
cd binarytree
go mod init binarytree

Defining the Binary Tree Node Structure

In Golang, we define the structure of a node in a binary tree:

package main

import "fmt"

type Node struct {
	Value int
	Left  *Node
	Right *Node
}

func NewNode(value int) *Node {
	return &Node{
		Value: value,
		Left:  nil,
		Right: nil,
	}
}

Each node contains a value and pointers to its left and right children.

Creating a Binary Tree

We can create a binary tree by defining a function to insert nodes into the tree:

type BinaryTree struct {
	Root *Node
}

func NewBinaryTree() *BinaryTree {
	return &BinaryTree{
		Root: nil,
	}
}

func (bt *BinaryTree) Insert(value int) {
	if bt.Root == nil {
		bt.Root = NewNode(value)
	} else {
		insertNode(bt.Root, value)
	}
}

func insertNode(node *Node, value int) {
	if value < node.Value {
		if node.Left == nil {
			node.Left = NewNode(value)
		} else {
			insertNode(node.Left, value)
		}
	} else {
		if node.Right == nil {
			node.Right = NewNode(value)
		} else {
			insertNode(node.Right, value)
		}
	}
}

This code initializes a binary tree and provides an Insert method to add nodes to the tree.

Searching for Elements in the Binary Tree

To search for an element, we recursively navigate through the tree:

func (bt *BinaryTree) Search(value int) *Node {
	return searchNode(bt.Root, value)
}

func searchNode(node *Node, value int) *Node {
	if node == nil || node.Value == value {
		return node
	}
	if value < node.Value {
		return searchNode(node.Left, value)
	}
	return searchNode(node.Right, value)
}

This function returns the node if it exists or nil if it does not.

Deleting Elements from the Binary Tree

To delete an element, we need to handle three cases: deleting a leaf node, deleting a node with one child, and deleting a node with two children:

func (bt *BinaryTree) Delete(value int) {
	bt.Root = deleteNode(bt.Root, value)
}

func deleteNode(node *Node, value int) *Node {
	if node == nil {
		return nil
	}
	if value < node.Value {
		node.Left = deleteNode(node.Left, value)
	} else if value > node.Value {
		node.Right = deleteNode(node.Right, value)
	} else {
		if node.Left == nil {
			return node.Right
		} else if node.Right == nil {
			return node.Left
		}

		minNode := findMin(node.Right)
		node.Value = minNode.Value
		node.Right = deleteNode(node.Right, minNode.Value)
	}
	return node
}

func findMin(node *Node) *Node {
	current := node
	for current.Left != nil {
		current = current.Left
	}
	return current
}

This code ensures the binary tree remains balanced and all references to the deleted node are properly updated.

Traversal Techniques

Traversing a binary tree means visiting all the nodes in a specific order. The most common traversal techniques are:

• In-order Traversal: Left, Root, Right
• Pre-order Traversal: Root, Left, Right
• Post-order Traversal: Left, Right, Root

In-order Traversal

func (bt *BinaryTree) InOrderTraversal(node *Node) {
	if node != nil {
		bt.InOrderTraversal(node.Left)
		fmt.Print(node.Value, " ")
		bt.InOrderTraversal(node.Right)
	}
}

Pre-order Traversal

func (bt *BinaryTree) PreOrderTraversal(node *Node) {
	if node != nil {
		fmt.Print(node.Value, " ")
		bt.PreOrderTraversal(node.Left)
		bt.PreOrderTraversal(node.Right)
	}
}

Post-order Traversal

func (bt *BinaryTree) PostOrderTraversal(node *Node) {
	if node != nil {
		bt.PostOrderTraversal(node.Left)
		bt.PostOrderTraversal(node.Right)
		fmt.Print(node.Value, " ")
	}
}

When Binary Trees Become Inefficient

While binary trees can achieve O(log n) time complexity for search, insertion, and deletion operations, this is only true for balanced trees. In the worst-case scenario, where the tree becomes completely unbalanced (e.g., a linked list), the time complexity can degrade to O(n). This can happen if elements are inserted in sorted order.

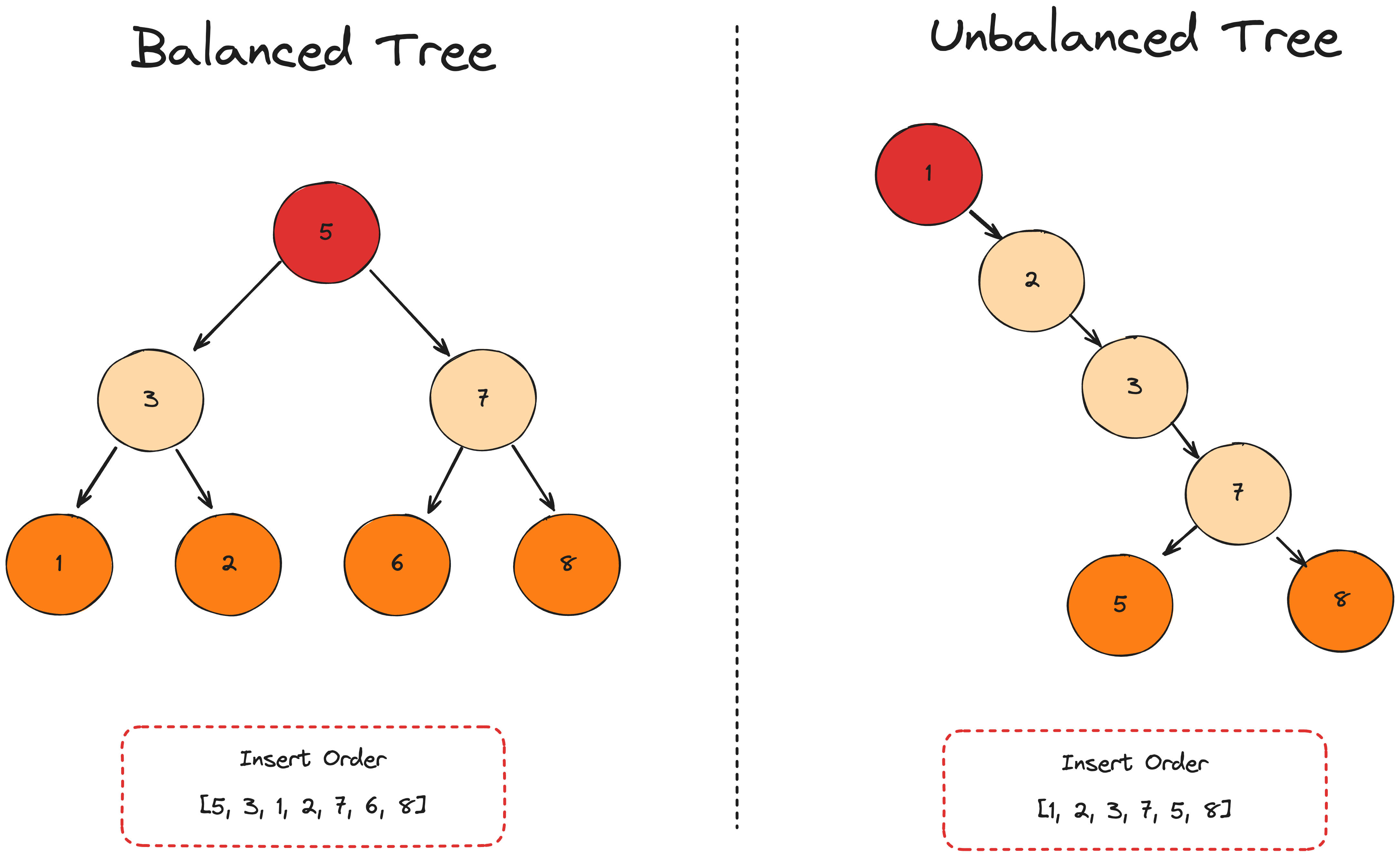
Towards Balance: What's Next?

To address the issue of unbalanced trees, several self-balancing binary tree algorithms have been developed, such as Red-Black Trees, AVL Trees, and B-Trees. These algorithms ensure that the tree remains balanced, providing guaranteed O(log n) time complexity for operations.

In our upcoming posts, we will explore these self-balancing binary trees and their implementations in Golang, starting with Red-Black Trees. Stay tuned!

Conclusion

In this post, we embarked on a quest to transform our data structures from O(n) to O(log n) time complexity. We learned about binary trees, their implementation in Golang, and their benefits. However, we also discovered the limitations of binary trees when they become unbalanced.

Stay tuned for our next post, where we will dive into implementing a Red-Black Tree in Golang, a self-balancing binary tree that ensures efficient operations.