Entendendo Calibração de Modelos

Em Machine Learning, ter um modelo que faz boas previsões não é suficiente, é necessário que as probabilidades sejam confiáveis. Imagine o seguinte, você criou um modelo que prevê o cancelamento de um cliente, seu modelo diz que há 75% de chance de um cliente cancelar. Sendo assim, para todos os clientes que você gerou essa previsão, cerca de 80% deles cancelaram.

Neste artigo, vamos explorar o que é calibração, por que ela é importante e como aplicá-la para melhorar a confiança nas previsões probabilísticas dos modelos.

O que é calibração de modelo?

A idéia por trás da calibração é bem simples, é alinhar as previsões do modelo com as probabilidades reais. Sendo assim, nós adicionamos um "post-processing" , um processo de refinamento da saída gerada do modelo treinado após a previsão.

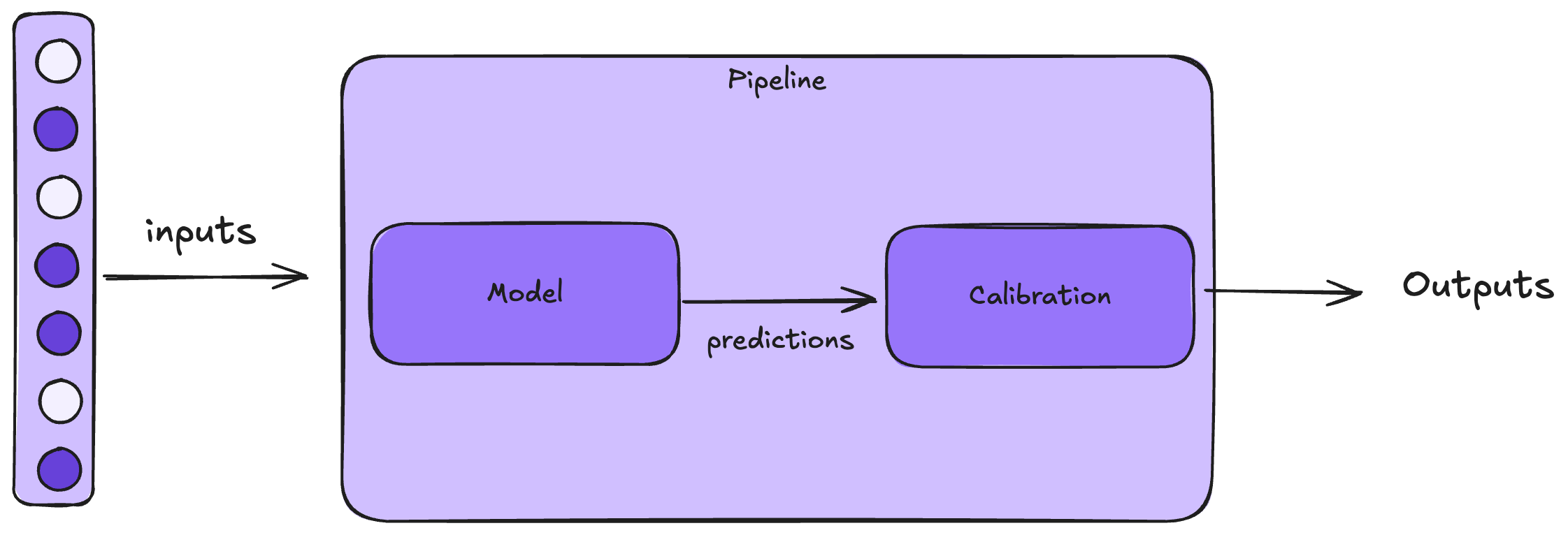
Por que calibração é importante?

Vamos para mais um exemplo, imagine uma empresa que oferece um serviço de assinatura. O time de dados desenvolve um modelo para prever o churn, ou seja, quais clientes estão propensos a cancelar o serviço. O modelo prevê que há 80% de chance de determinados clientes cancelarem no próximo mês. No entanto, ao revisar os dados reais, percebe-se que apenas 50% desses clientes realmente cancelaram.

Agora, pense nas consequências: uma equipe de marketing pode gastar tempo e recursos criando campanhas para reter clientes que, na verdade, não estavam prestes a cancelar. Ou pior, ignorar clientes que deveriam ser priorizados. Com um modelo bem calibrado, as previsões se alinham melhor à realidade, permitindo decisões mais assertivas.

Aqui estão mais cenários onde calibração faz toda a diferença:

• Finanças: Uma instituição financeira usa modelos para decidir se aprova um empréstimo. Um modelo calibrado garante que as probabilidades previstas de inadimplência reflitam a realidade, minimizando riscos e maximizando lucros.
• Saúde: Um hospital utiliza modelos para estimar a gravidade de um caso. Se o modelo indica que um paciente tem alta probabilidade de precisar de cuidados intensivos, é essencial que isso corresponda à realidade para priorizar recursos adequadamente.
• Segurança: Plataformas de pagamento online empregam modelos para detectar fraudes. Um modelo mal calibrado pode gerar falsos positivos, causando inconvenientes aos usuários, ou falsos negativos, expondo a empresa a perdas financeiras.

Quando as probabilidades previstas estão alinhadas às probabilidades reais, as decisões baseadas nelas são não apenas mais confiáveis, mas também mais eficazes.

Como identificar se um modelo está calibrado?

Você consegue visualizar se o modelo está calibrado através do gráfico Reliability Diagram, caso o modelo esteja calibrado, a linha Reliability Diagram deve estar próxima da diagonal , onde as previsões correspondem à realidade observada.

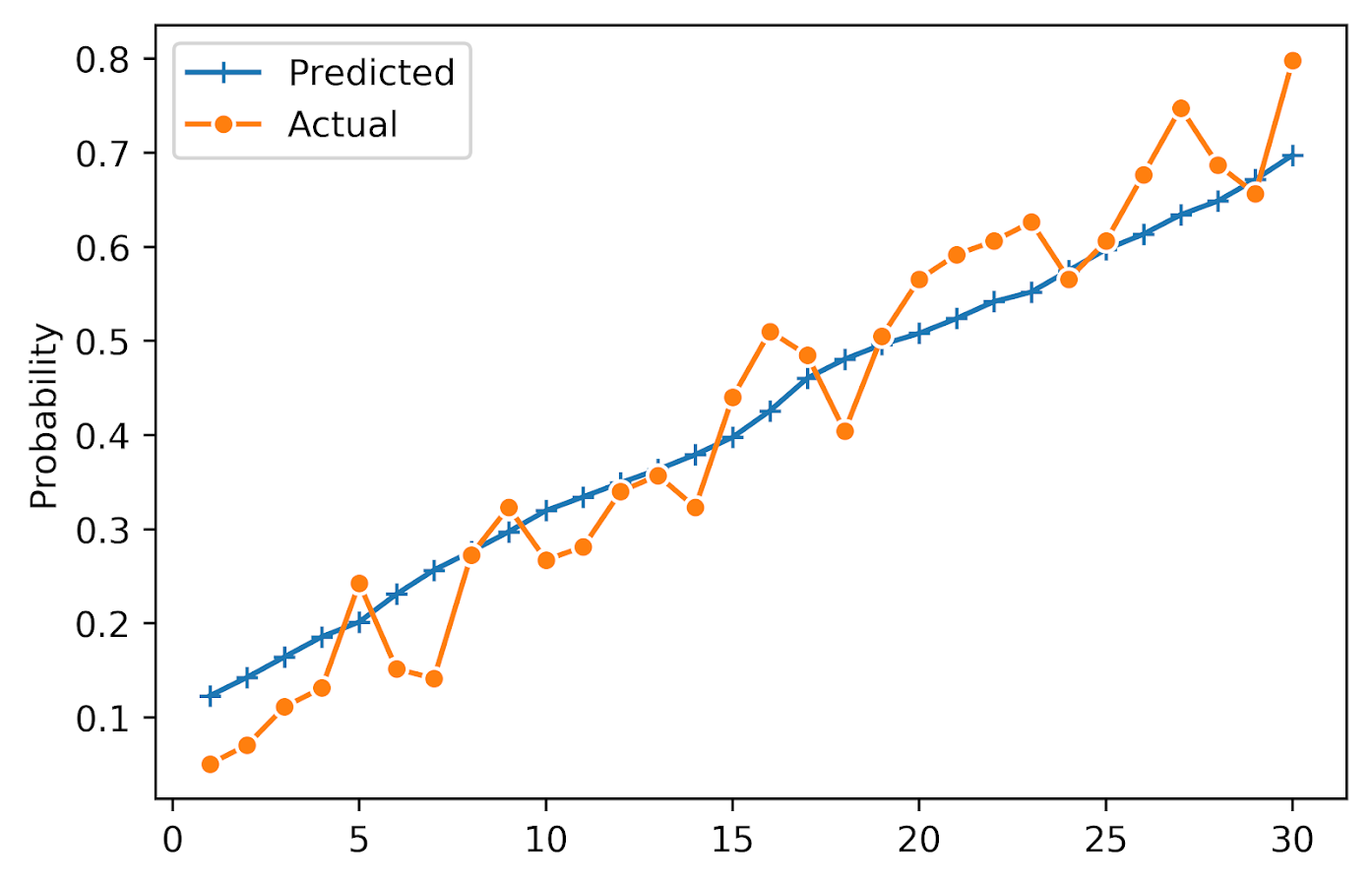
Para gerar esse gráfico é bem simples, você pode usar a função calibration_curve do sklearn, onde recebe os dados reais e as previsões e pronto, só plotar utilizando o matplotlib

import numpy as np
from sklearn.calibration import calibration_curve
import matplotlib.pyplot as plt

# Simulando previsões e valores reais
y_true = np.random.binomial(1, 0.7, size=1000)  # Verdadeiros
y_pred = np.random.uniform(0, 1, size=1000)     # Previsões

# Calculando o Reliability Diagram
prob_true, prob_pred = calibration_curve(y_true, y_pred, n_bins=10)

# Plotando o gráfico
plt.plot(prob_pred, prob_true, marker='o', label='Modelo')
plt.plot([0, 1], [0, 1], linestyle='--', label='Ideal')
plt.xlabel('Previsão')
plt.ylabel('Frequência Observada')
plt.legend()
plt.title('Reliability Diagram')
plt.show()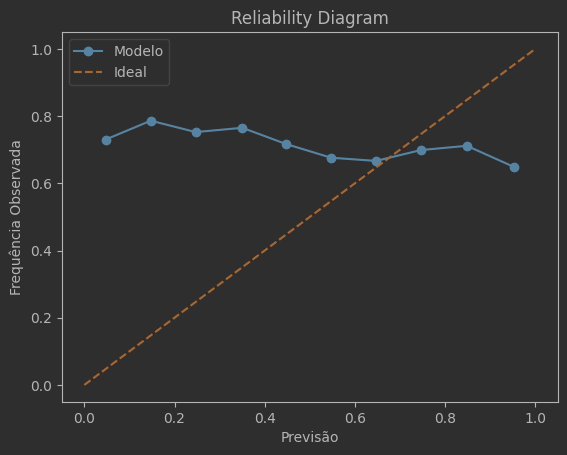

Métricas para medir calibração

Além dos gráficos podemos usar métricas que mensuram o quanto o nosso modelo está descalibrado, com isso fica mais fácil compara abordagens e modelos diferentes.

1. Log Loss

A primeira métrica é a Log Loss, ela é uma transformação logarítmica da função de verossimilhança, usada principalmente para avaliar o desempenho de classificadores probabilísticos.

Ele mede a "penalidade" das previsões erradas, com foco especial nas previsões muito confiantes, essa é a sua formula:

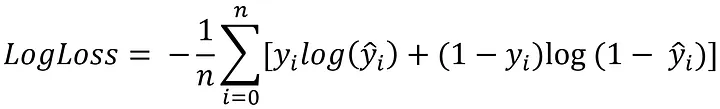
Onde:

• yi: Valor real da classe (0 ou 1).
• ^yi: Probabilidade prevista para a classe 1.

Quanto menor o Log Loss, melhor é a calibração do modelo, essa métrica é utilizada em cenários que previsões erradas tem consequências graves.

2. Brier Score

Diferentemente da Log Loss, que penaliza severamente previsões erradas, o Brier Score considera apenas o erro quadrático, sendo mais sensível a pequenos desvios. Ele é particularmente útil em modelos que geram probabilidades para situações onde a calibração global é mais relevante.

Essa é a formula:

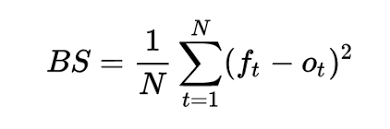
Onde:

• ft: Valor real da classe (0 ou 1)
• ot: Probabilidade prevista para a classe 1.

Diferenças entre Log Loss e Brier Score:

• Log Loss: Penaliza mais previsões confiantes e erradas.
• Brier Score: Foca no erro absoluto, sem priorizar previsões confiantes.

from sklearn.metrics import log_loss, brier_score_loss

log_loss_value = log_loss(y_true, y_pred)
brier_score = brier_score_loss(y_true, y_pred)

print(f'Log Loss: {log_loss_value:.4f}')
print(f'Brier Score: {brier_score:.4f}')

Com essas métricas, você pode medir objetivamente quão bem calibrado está o seu modelo.

Técnicas de Calibração

Depois que diagnosticamos e notamos que o nosso modelo não está calibrado, podemos usar algumas técnicas para ajusta-lo, elas são métodos de pós-processamento usado para calibrar as estimativas de probabilidade de um classificador binário.

Platt Scaling

Platt Scaling foi apresentado pela primeira vez para calibrar SVMs (Máquina de Vetores de Suporte) pelo John Platt, hoje ele é amplamente utilizado para calibrar vários tipos de classificadores. Essencialmente, Platt Scaling é uma regressão logística aplicada às previsões do modelo.

A fórmula é:

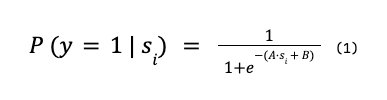
A e B são parâmetros da função e são obtidos através da minimização da Log Loss que comentei anteriormente.

Vantagens

• Poucos dados necessários: Ele não exige uma grande quantidade de dados para realizar o ajuste.
• Funciona bem em condições gaussianas: Se as pontuações das classes seguirem distribuições gaussianas com variâncias iguais.

Desvantagens

• Não resolve tudo: Se o ajuste exigir correções não monotônicas, Platt Scaling pode não ser suficiente.

Platt tem a vantagem de não exigir que muitos dados sejam treinados e funciona bem quando as distribuições de pontuações das classes seguem padrões semelhantes, como distribuições gaussianas com variância iguais.

No entanto, também tem duas grandes desvantagens: não pode fornecer boas calibrações quando correções não monotônicas são necessárias (isso é compartilhado com a escala de Platt) e geralmente requer uma vasta quantidade de dados em comparação com métodos paramétricos, pois é propenso a overfitting.

Isotonic Regression

Essa abordagem não assume um formato fixo para o ajuste e usa uma função de mapeamento não linear para recalibrar as probabilidades. É mais flexível, mas requer mais dados para evitar overfitting.

A Isotonic Regression é uma técnica que não faz suposições sobre as distribuições das previsões. Ela simplesmente ajusta os valores previstos para que eles sejam sempre "crescentes" de forma consistente com os resultados reais. Isso é ótimo para garantir que as probabilidades previstas por um modelo reflitam corretamente a relação com as observações verdadeiras.

Agora, você pode estar se perguntando: "Mas o que significa essa tal de monotonicamente crescente?".

Basicamente, é quando as previsões seguem uma ordem lógica: à medida que a probabilidade de um evento aumenta, os resultados observados também acompanham essa tendência, sem "voltas" ou "recuos" desnecessários.

A formula segue:

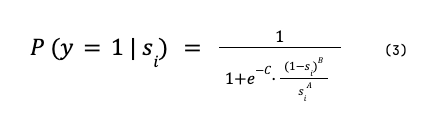
Assim como Platt, A e B são parâmetros da função e são obtidos através da minimização da Log Loss.

Vantagens

• Flexibilidade : Não assume uma forma específica para a função de calibração, tornando-a mais adaptável a diferentes distribuições de dados.
• Calibração aprimorada : geralmente fornece melhor calibração para modelos e conjuntos de dados complexos.

Limitações

• Overfitting : Mais propenso a overfitting, especialmente com dados limitados.
• Previsões constantes por partes : podem produzir estimativas de probabilidade menos suaves em comparação com a escala de Platt.

Calibrando o modelo

Chega de teoria, vamos botar a mão na massa, vamos iniciar treinando o nosso modelo normalmente, Este modelo inicial fornecerá previsões, mas ainda não está calibrado, ou seja, as probabilidades podem não refletir a realidade.

Logo depois vamos usar a classe CalibratedClassifierCV, que receberá o nosso modelo inicial e ela tem mais dois parâmetros importantes:

• O parâmetro method='sigmoid' indica que estamos usando o Platt Scaling e method='isotonic' estaremos usando Isotonic Regression.
• Se o modelo já foi treinado anteriormente, podemos usar o cv='prefit', caso contrário podemos informar o tamanho do cross validation cv=10.

from sklearn.calibration import CalibratedClassifierCV
from sklearn.ensemble import GradientBoostingClassifier

# Treinando um modelo base
model = GradientBoostingClassifier()
model.fit(X_train, y_train)

# Calibrando com Platt Scaling
calibrated_model_platt = CalibratedClassifierCV(model, method='sigmoid', cv= 'prefit')
calibrated_model_platt.fit(X_train, y_train)


# Calibrando com Isotonic Regression
calibrated_model_isotonic = CalibratedClassifierCV(model, method='isotonic', cv= 'prefit' )
calibrated_model_isotonic.fit(X_train, y_train)

Agora que os nossos modelos estão calibrado, podemos gear as probabilidades e mensurar o quão bom o nosso modelo está bom usando o Brier Score.

# Prevê probabilidades no conjunto de teste
 probabilities_platt = calibrated_model_platt.predict_proba(X_test)[:, 1 ] 
 probabilities_isotonic = calibrated_model_isotonic.predict_proba(X_test)[:, 1 ] 

# Calcula a pontuação de Brier
 brier_score_platt = brier_score_loss(y_test, probabilities_platt) 
print ( f'Brier Score Platt: {brier_score} ' ) 
 brier_score_platt = brier_score_loss(y_test, probabilities_isotonic) 
print ( f'Brier Score Isotonic: {brier_score} ' ) 

Vamos deixar esse resultado mais visual, então vamos plotar o gráfico de calibração (Reliability Diagram).

Para isso usaremos a função calibration_curve para gerar a fração real de eventos positivos (prob_true) e a Probabilidade média prevista (prob_pred) para cada intervalo.

prob_true_platt, prob_pred_platt = calibration_curve(
  y_test, 
  probabilities_platt, 
  n_bins= 10
) 

prob_true_isotonic, prob_pred_isotonic = calibration_curve(
  y_test, 
  probabilities_isotonic, 
  n_bins= 10
) 

plt.figure(figsize=( 10 , 6 )) 
plt.plot(prob_pred_isotonic, prob_true_isotonic, marker= 'o' , label= 'Regressão Isotônica' ) 
plt.plot(prob_pred_isotonic, prob_true_isotonic, marker= 'o' , label= 'Platt' ) 
plt.plot([ 0 , 1 ], [ 0 , 1 ], linestyle= '--' , label= 'Perfeitamente Calibrado' ) 
plt.xlabel( 'Probabilidade Média Prevista' ) 
plt.ylabel( 'Fração de Positivos' ) 
plt.title( 'Gráfico de Calibração (Diagrama de Confiabilidade)' ) 
plt.legend() 
plt.show()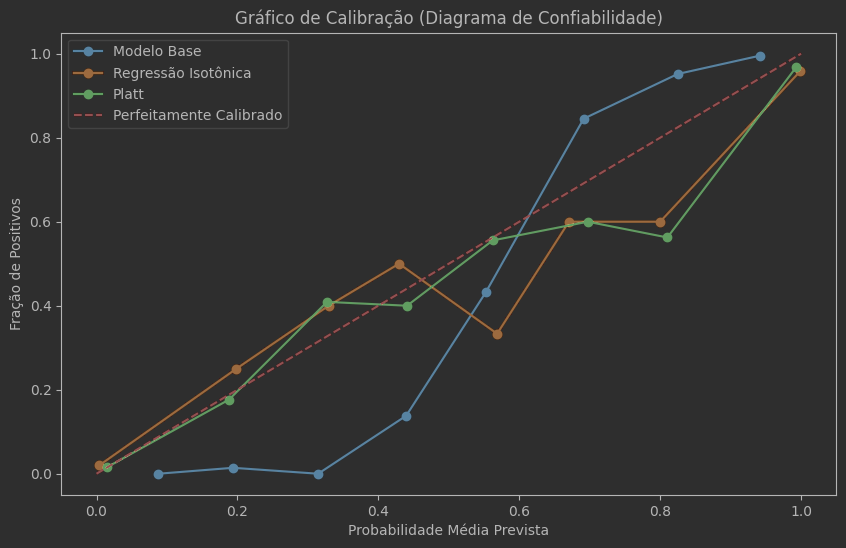

Conclusão

Concluindo, a calibração é uma peça essencial em Machine Learning, garantindo não apenas a precisão das previsões, mas também a confiabilidade da confiança que atribuímos a elas. Um modelo bem calibrado não só melhora a qualidade das decisões, mas também fortalece a transparência e a confiança em sistemas de IA, especialmente em contextos críticos como saúde, finanças e segurança.

À medida que o aprendizado de máquina se torna cada vez mais central em decisões estratégicas, entender e aplicar técnicas de calibração será uma habilidade indispensável. Seja utilizando Platt Scaling ou Isotonic Regression, o objetivo final é o mesmo: alinhar as previsões do modelo com a realidade, criando sistemas mais robustos e confiáveis. Por isso, investir em calibração é investir em decisões melhores e mais bem informadas.

Referências

1. Platt, J. (2000). Probabilities for SV machines. In Advances in Large Margin Classifiers (A. Smola, P. Bartlett, B. Schölkopf and D. Schuurmans, eds.) 61–74. MIT Press.

2. Kull, M., Silva Filho, T., Flach, P. (2017). Beyond sigmoids: How to obtain well-calibrated probabilities from binary classifiers with beta calibration. Electron. J. Statist. 11, no. 2, 5052–5080. doi: 10.1214/17-EJS1338SI.

3. Niculescu-Mizil, Alexandru, and Rich Caruana. "Predicting good probabilities with supervised learning." Proceedings of the 22nd international conference on Machine learning. 2005.